개요
- 대표적인 그래프 탐색 알고리즘
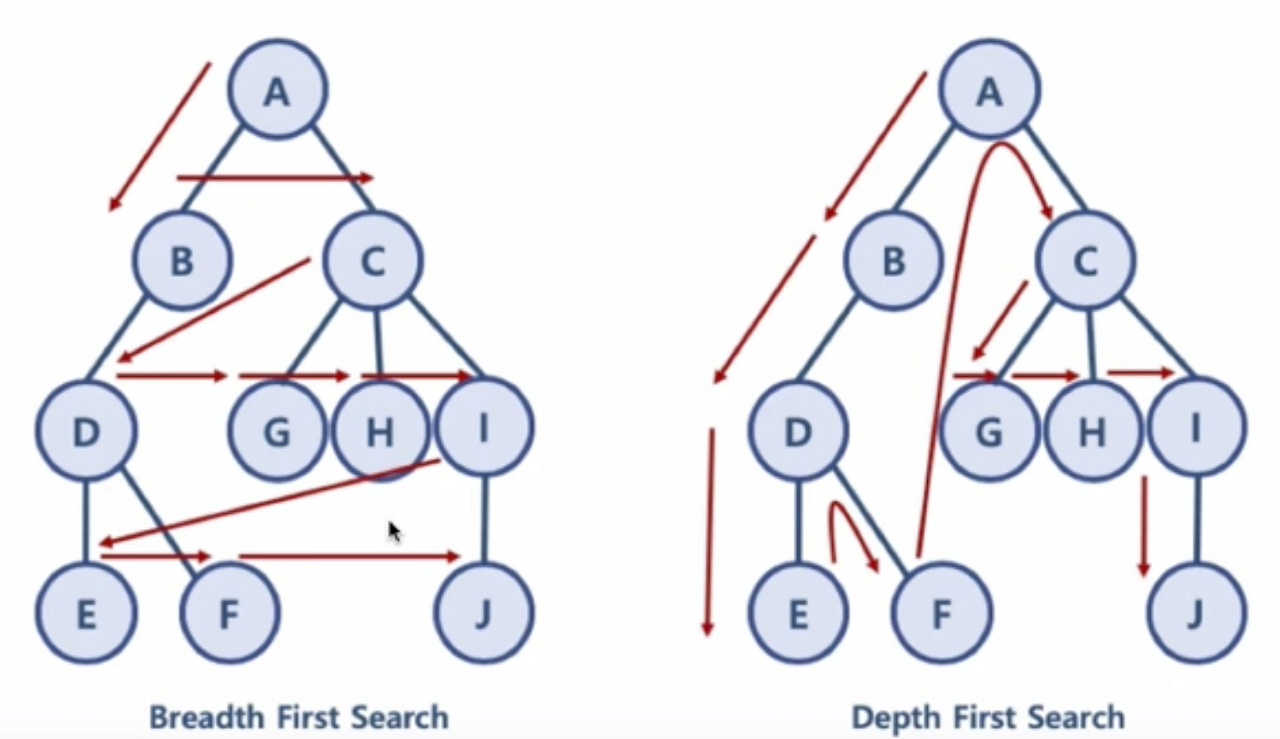
- 너비 우선 탐색 (BFS, Breadth-First Search): 노드들과 같은 레벨에 있는 노드를 먼저 탐색하는 방식. 한 단계씩 내려가면서 같은 단계에 존재하는 노드들을 먼저 순회함.
- 깊이 우선 탐색 (DFS, Depth-First Search): 노드의 자식들을 먼저 탐색하는 방식. 한 노드 의 자식을 타고 끝까지 순회한 후, 다시 돌아와 다른 노드들의 자식을 타고 내려가며 순회함.
- 파이썬의 딕셔너리와 리스트 자료구조를 활용해 그래프를 표현 가능함
BFS (너비우선탐색, Breadth-First Search)
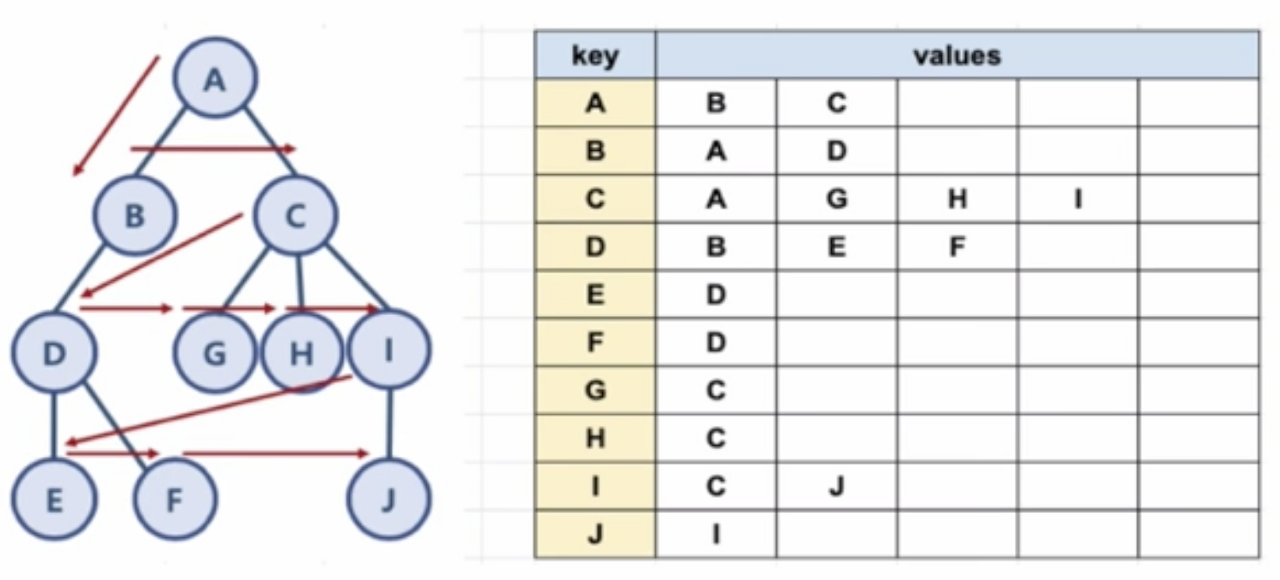
구현
- 방문할 노드(need_visti_queue)들과 방문한 노드(visited_queue)들을 append하는 두 개의 큐를 활용함
graph = dict()
graph["A"] = ["B", "C"]
graph["B"] = ["A", "D"]
graph["C"] = ["A", "G", "H", "I"]
graph["D"] = ["B", "E", "F"]
graph["E"] = ["D"]
graph["F"] = ["D"]
graph["G"] = ["C"]
graph["H"] = ["C"]
graph["I"] = ["C", "J"]
graph["J"] = ["I"]
def bfs(graph, start_node):
visted_queue = list()
need_visit_queue = list()
need_visit_queue.append(start_node)
while need_visit_queue:
node = need_visit_queue.pop(0)
if node not in visted_queue:
visted_queue.append(node)
need_visit_queue.extend(graph.get(node))
return visted_queue
print(bfs(graph, "A"))시간 복잡도
노드 수가 V, 간선 수가 E 일 때 O(V+E)의 시간복잡도를 갖는다. (while need_visit_queue를 V+E만큼 수행하기 때문에)
DFS (깊이우선탐색, Depth-First Search)

구현
- 자료구조 스택과 큐를 활용함.
- BFS는 need_visit과 visited 모두 큐였지만 DFS에서는 need_visit을 스택으로 생성한다.
graph = dict()
graph["A"] = ["B", "C"]
graph["B"] = ["A", "D"]
graph["C"] = ["A", "G", "H", "I"]
graph["D"] = ["B", "E", "F"]
graph["E"] = ["D"]
graph["F"] = ["D"]
graph["G"] = ["C"]
graph["H"] = ["C"]
graph["I"] = ["C", "J"]
graph["J"] = ["I"]
def dfs(graph, start_node):
visted_queue = list()
need_visit_stack = list()
need_visit_stack.append(start_node)
while need_visit_stack:
node = need_visit_stack.pop()
if node not in visted_queue:
visted_queue.append(node)
need_visit_stack.extend(graph.get(node))
return visted_queue
print(dfs(graph, "A"))BFS, DFS 구현에서의 차이
- need_visit이 BFS에서는 queue(FIFO)이고 DFS에서는 stack(FILO, LIFO)이다. 그래서 방문했는지 확인하는 노드를 가져올 때 need_visit에 젤 처음 들어온 노드를 꺼내느냐, 마지막으로 들어온 노드를 꺼내느냐의 차이가 발생함
시간복잡도
- BFS와 동일하게 O(노드수+간선수)임.
'Computer Science > Data Structure & Algorithm' 카테고리의 다른 글
| 그래프 (0) | 2022.05.30 |
|---|---|
| 병합정렬 (Merge sort) (0) | 2022.04.17 |
| 퀵정렬 (Quick sort) (0) | 2022.04.17 |
| 동적계획법(Dynamic Programming)과 분할정복 (Divide and Conquer) (0) | 2022.04.10 |
| 힙 (Heap) (0) | 2022.03.27 |